Section outline

  • The path of the sun around the Earth.

    The first science developed by humans is probably astronomy. Before the invention of clocks and calendars, early people looked to the night sky to help them keep track of time. What is the best time to plant crops, and when will they ripen? On what day exactly do important religious festivals fall? By tracking the motions of the stars, early astronomers could identify the summer and winter solstices and the equinoxes. The rising and setting of certain stars marked the hours of the night. If we think of the stars as traveling on a dome above the Earth, we create the celestial sphere. Actually, of course, the Earth itself rotates among the stars, but for calculating the motions of heavenly objects, this model works very well.

    Babylonian astronomers kept detailed records on the motion of the planets, and were able to predict solar and lunar eclipses. All of this required familiarity with angular distances measured on the celestial sphere. To find angles and distances on this imaginary sphere, astronomers invented techniques that are now part of spherical trigonometry. The laws of sines and cosines were first stated in this context, in a slightly different form than the laws for plane trigonometry.

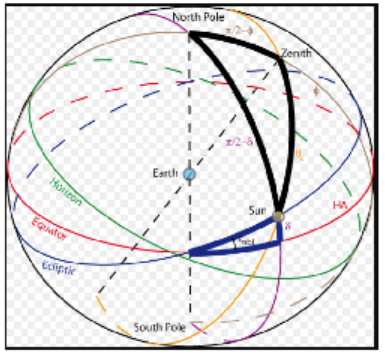
    On a sphere, a great-circle lies in a plane passing through the sphere's center. It gives the shortest distance between any two points on a sphere, and is the analogue of a straight line on a plane. A spherical angle is formed where two such arcs intersect, and a spherical triangle is made up of three arcs of great circles. The spherical law of sines was first introduced in Europe in 1464 by Johann Muller, also known as Regiomontus, who wrote: "You, who wish to study great and wondrous things, who wonder about the movement of the stars, must read these theorems about triangles. ... For no one can bypass the science of triangles and reach a satisfying knowledge of the stars."

    Image Caption: Representation of the declination and of the hour angle in a geocentric system. On this figure, the equator and the ecliptic are fixed. The apparent motion of the Sun corresponds to a complete revolution along the ecliptic in one year. The hour angle (and the location of the local meridian (brown circle) trough the North pole and the zenith) change as the Earth makes a complete rotation around its axis in 1 day. (credit: Universite catholique de Louvain, http://www.climate.be/textbook/chapter2_node5_2.xml, CC BY-BC License)

    (Content & Image Source: Chapter 3 Introduction, Trigonometry, Katherine Yoshiwara, GNU Free Documentation License)

    Upon completion of this module, you will be able to: 

    3.1 Obtuse Angles
    • Use the coordinate definition of the trig ratios
    • Find the trig ratios of supplementary angles
    • Know the trig ratios of the special angles in the second quadrant
    • Find two solutions of the equation sin( \theta)=k
    • Find the area of a triangle
    3.2 The Law of Sines
    • Use the Law of Sines to find a side
    • Use the Law of Sines to find an angle
    • Use the Law of Sines to solve an oblique triangle
    • Solve problems using the Law of Sines
    • Compute distances using parallax
    • Solve problems involving the ambiguous case
    3.3 The Law of Cosines
    • Use the Law of Cosines to find the side opposite an angle
    • Use the Law of Cosines to find an angle
    • Use the Law of Cosines to find a side adjacent to an angle
    • Decide which law to use
    • Solve a triangle
    • Solve problems using the Law of Cosines
    To achieve these objectives:
    1. Read the Module 3 Introduction (see above).
    2. Read Sections 3.1-3.3 of Chapter 3: Laws of Sines and Cosines in Trigonometry (links to each Section provided below)
      • Note: The Algebra Refresher at the top of each Section might be beneficial before you begin
      • At the end of each Section there is a list of Vocabulary, Concepts, Study Questions, and a Self-Check H5P activity
    3. Complete the MyOpenMath Homework Assignments for each Section (links provided below) - These are graded!
    4. View the Chapter 3 Summary and Review (link provided below)
    5. Practice the problems on the Exercises Sections, checking the solutions provided (links to each Section provided below)
    6. View the Exercises: Chapter 3 Review Problems (link provided below)
    7. Complete the MyOpenMath Quiz for Chapter 3 (link provided below) - This is graded!
    8. Once you complete the Quiz, upload your work in the Quiz Work Upload Assignment using the submission link below.
    9. Post in the Chapter 3 Q&A Discussion Forum - link provided below.

    Note the check boxes to the right that help you track your progress: some are automatic, and some are manual.

    Module Pressbooks Resources and Activities

    You will find the following resources and activities in this module at the Pressbooks website. Click on the links below to access or complete each item.
Accessibility
Reset All

Background Colour Background Colour

Font Face Font Face

Font Kerning Font Kerning

Font Size Font Size

1

Image Visibility Image Visibility

Letter Spacing Letter Spacing

0

Line Height Line Height

1.2

Link Highlight Link Highlight

Text Colour Text Colour