Section outline

  • Geometric designs

    Have you ever wonderd why we divide the circle into 360 degrees? Nobody really knows the answer, but it may well have started around 600 BCE with the Babylonians. The Babylonians lived between the Tigris and Euphrates rivers in present day Turkey and Syria. They kept written records using a stylus to press cuneiform, or wedge-shaped, symbols into wet clay tablets, which were then baked in the sun. Thousands of these tablets have survived and give us detailed information about the mathematical practices of the time. 

    The Babylonians used a base 60 number system because the number 60 has many factors. They did not invent decimal fractions, so they found it difficult to deal with remainders when doing division. But 60 can be divided evenly by 2, 3, 4, 5, and 6, which made calculations with common fractions much easier. We still see traces of their base 60 system in our own day: there are 60 seconds in a minute, and 60 minutes in an hour.

    In geometry, Babylonian mathematicians used the corner of an equilateral triangle as their basic unit of angular measure, and naturally divided that angle into 60 smaller angles. Now, if the corners of six equilateral triangles are placed together they form a complete circle, and that is why there are six times 60, or 360 degrees of arc in a circle. During the reign of Nebuchadnezzar, using the tools and technology available to them, Babylonian astronomers calculated that a complete year numbered 360 days. This made dividing the circle into 360 degrees even more useful. So the number 360 is not fundamental to the nature of a circle. If ancient civilizations had defined the full circle to be some other number of degrees, we'd probably be using that number today. But why do we need another, different way to measure angles? In this chapter we'll study radian measure, which at first may seem awkward and unnatural. As a hint, consider that although 360 is not fundamental to circles, the number is.

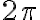
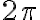    Radians connect the measure of an angle with the arc-length it cuts out on a circle. Imagine a circle of radius 1unit rolling along a straight line. The circumference of a circle is  2 \pi times the length of its radius, so when the circle has turned through one complete revolution, it has traveled a distance of 2 \pi units. When the circle has turned through half a revolution, it has traveled a distance of 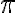\pi units. In radian measure, the angle through which the circle has turned is equal to the distance the circle has traveled, or the length of the arc that has unrolled on the line. The idea of radian measure was developed by Roger Cotes, an English mathematician who worked closely with Isaac Newton. He described the radian in everything but name, and recognized its naturalness as a unit of angular measure.

    The term radian first appeared in print on June 5, 1873, on an exam written by James Thomson, the brother of Lord Kelvin, at Queen's College in Belfast. In calculus and most other branches of mathematics beyond practical geometry, angles are nearly always measured in radians. Because radians arise naturally when dealing with circles, important relationships are expressed more concisely in radians. In particular, results involving trigonometric functions are simpler when the variables are expressed in radians.

    Image Caption: None

    (Content & Image Source: Chapter 6 Introduction, Trigonometry, Katherine Yoshiwara, GNU Free Documentation License)

    Upon completion of this module, you will be able to: 

    6.1 Arclength and Radians
    • Express angles in degrees and radians
    • Sketch angles given in radians
    • Estimate angles in radians
    • Use the arclength formula
    • Find coordinates of a point on a unit circle
    • Calculate angular velocity and area of a sector
    6.2 The Circular Functions
    • Know the trigonometric function values for the special angles in radians
    • Use a unit circle to find trig values
    • Find reference angles in radians
    • Evaluate trigonometric expressions
    • Find coordinates on a unit circle
    • Find an angle with a given terminal point on a unit circle
    • Use the tangent ratio to find slope
    • Find coordinates on a circle of radius
    6.3 Graphs of the Circular Functions
    • Graph the trig functions of real numbers
    • Solve trigonometric equations graphically
    • Work with reference angles
    • Solve trigonometric equations algebraically
    • Evaluate trigonometric functions of real numbers
    • Use trigonometric models
    • Locate points on the graphs of the trigonometric functions
    • Find the domain and range of a function
    To achieve these objectives:
    1. Read the Module 6 Introduction (see above).
    2. Read Sections 6.1-6.3 of Chapter 6: Radians in Trigonometry (links to each Section provided below)
      • Note: The Algebra Refresher at the top of each Section might be beneficial before you begin
      • At the end of each Section there is a list of Vocabulary, Concepts, Study Questions, and a Self-Check H5P activity
    3. Complete the MyOpenMath Homework Assignments for each Section (links provided below) - These are graded!
    4. View the Chapter 6 Summary and Review (link provided below)
    5. Practice the problems on the Exercises Sections, checking the solutions provided (links to each Section provided below)
    6. View the Exercises: Chapter 6 Review Problems (link provided below)
    7. Complete the MyOpenMath Quiz for Chapter 6 (link provided below) - This is graded!
    8. Once you complete the Quiz, upload your work in the Quiz Work Upload Assignment using the submission link below.
    9. Post in the Chapter 6 Q&A Discussion Forum - link provided below.

    Note the check boxes to the right that help you track your progress: some are automatic, and some are manual.

    Module Pressbooks Resources and Activities

    You will find the following resources and activities in this module at the Pressbooks website. Click on the links below to access or complete each item.
Accessibility
Reset All

Background Colour Background Colour

Font Face Font Face

Font Kerning Font Kerning

Font Size Font Size

1

Image Visibility Image Visibility

Letter Spacing Letter Spacing

0

Line Height Line Height

1.2

Link Highlight Link Highlight

Text Colour Text Colour