Module 8: More Functions and Identities (Chapter 8)
Section outline
-
 Mapmakers have always faced an unavoidable challenge: It is impossible
to translate the surface of a sphere onto a flat map without some form
of distortion. Over the years, a variety of map projections have been
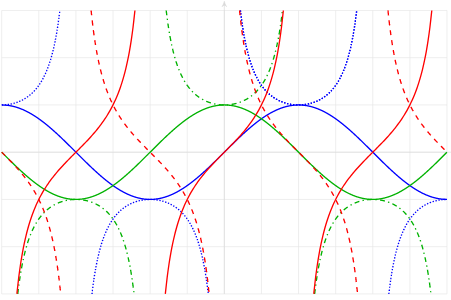
developed to suit different uses.The sixteenth century was an age of discovery, when explorers and merchants began sailing to distant and previously unknown lands. But at that time there was no reliable technology for navigation.Although more regions of the world were being mapped more accurately, a flat map by itself was not enough to help a sailor in the middle of the ocean. In 1569, the Flemish cartographer Gerardus Mercator published a new map using what is known as a cylindrical projection. To imagine how a Mercator projection works, picture shining a light through a glass globe onto a piece of paper rolled into a cylinder and wrapped around the globe. The cylinder is tangent to the globe at its equator. Notice how the latitude lines are farther apart the farther you get from the Equator. This projection distorts the size of objects as the latitude increases, so that Greenland and Antarctica appear much larger than they actually are.But the Mercator projection map is ideally suited for navigation, because any straight line on the map is a line of constant true bearing. If a navigator measures the bearing on the map from his location to his destination, he can set his ship's compass for the same bearing and maintain that course. However, the Mercator projection does not preserve distances. On a globe, circles of latitude (also known as parallels) get smaller as they move away from the Equator towards the poles. Thus, in the Mercator projection, when a globe is "unwrapped" on to a rectangular map, the parallels need to be stretched to the length of the Equator. Mercator had to increase the scale of his map gradually as it moved away from the equator, so that the latitude lines appear equal in length to the equator.The horizontal scale factor at any latitude must be inversely proportional to lengths on that latitude. Because the radius of the circle of latitude
Mapmakers have always faced an unavoidable challenge: It is impossible
to translate the surface of a sphere onto a flat map without some form
of distortion. Over the years, a variety of map projections have been
developed to suit different uses.The sixteenth century was an age of discovery, when explorers and merchants began sailing to distant and previously unknown lands. But at that time there was no reliable technology for navigation.Although more regions of the world were being mapped more accurately, a flat map by itself was not enough to help a sailor in the middle of the ocean. In 1569, the Flemish cartographer Gerardus Mercator published a new map using what is known as a cylindrical projection. To imagine how a Mercator projection works, picture shining a light through a glass globe onto a piece of paper rolled into a cylinder and wrapped around the globe. The cylinder is tangent to the globe at its equator. Notice how the latitude lines are farther apart the farther you get from the Equator. This projection distorts the size of objects as the latitude increases, so that Greenland and Antarctica appear much larger than they actually are.But the Mercator projection map is ideally suited for navigation, because any straight line on the map is a line of constant true bearing. If a navigator measures the bearing on the map from his location to his destination, he can set his ship's compass for the same bearing and maintain that course. However, the Mercator projection does not preserve distances. On a globe, circles of latitude (also known as parallels) get smaller as they move away from the Equator towards the poles. Thus, in the Mercator projection, when a globe is "unwrapped" on to a rectangular map, the parallels need to be stretched to the length of the Equator. Mercator had to increase the scale of his map gradually as it moved away from the equator, so that the latitude lines appear equal in length to the equator.The horizontal scale factor at any latitude must be inversely proportional to lengths on that latitude. Because the radius of the circle of latitude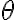 is
is 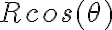
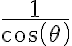
Upon completion of this module, you will be able to:8.1 Sum and Difference Formulas-
Find trig values for the negative of an angle
-
Verify or disprove possible formulas
-
Find exact values for trigonometric functions
-
Simplify or expand expressions
-
Solve equations
-
Prove standard identities
8.2 Inverse Trigonometric Functions-
Decide whether a function has an inverse function
-
Evaluate the inverse trig functions
-
Model problems with inverse trig functions
-
Solve formulas
-
Simplify expressions involving the inverse trig functions
-
Graph the inverse trig functions
8.3 The Reciprocal FunctionsTo achieve these objectives:-
Evaluate the reciprocal trig functions for angles in degrees or radians
-
Find values or expressions for the six trig ratios
-
Evaluate the reciprocal trig functions in applications
-
Given one trig ratio, find the others
-
Evaluate expressions exactly
-
Graph the secant, cosecant, and cotangent functions
-
Identify graphs of the reciprocal trig functions
-
Solve equations in secant, cosecant, and cotangent
-
Use identities to simplify or evaluate expressions
- Read the Module 8 Introduction (see above).
- Read Sections 8.1-8.3 of Chapter 8: More Functions and Identities in Trigonometry (links to each Section provided below)
- Note: The Algebra Refresher at the top of each Section might be beneficial before you begin
- At the end of each Section there is a list of Vocabulary, Concepts, Study Questions, and a Self-Check H5P activity
- Complete the MyOpenMath Homework Assignments for each Section (links provided below) - These are graded!
- View the Chapter 8 Summary and Review (link provided below)
- Practice the problems on the Exercises Sections, checking the solutions provided (links to each Section provided below)
- View the Exercises: Chapter 8 Review Problems (link provided below)
- Complete the MyOpenMath Quiz for Chapter 8 (link provided below) - This is graded!
- Once you complete the Quiz, upload your work in the Quiz Work Upload Assignment using the submission link below.
- Post in the Chapter 8 Q&A Discussion Forum - link provided below.
Note the check boxes to the right that help you track your progress: some are automatic, and some are manual.
Module Pressbooks Resources and Activities
You will find the following resources and activities in this module at the Pressbooks website. Click on the links below to access or complete each item.
-
Background Colour
Font Face
Font Kerning
Font Size
Image Visibility
Letter Spacing
Line Height
Link Highlight
Text Colour