Module 10: Polar Coordinates and Complex Numbers (Chapter 10)
Section outline
-
 The Barnsley fern is an example of a fractal. A fractal is an infinitely complex pattern created by iteration: repeating a process over and over in an ongoing feedback loop. One of the most famous and intriguing fractals is the Mandelbrot set, named after the French mathematician Benoît Mandelbrot, who lived from 1924 to 2010. The Mandelbrot set looks like a cardioid, or heart-shaped figure, studded with circles all around its boundary.Like the Barnsley fern, we can create the Mandelbrot set by repeatedly evaluating a simple equation over and over. This equation uses complex numbers. The plane of complex numbers is similar to a two dimensional coordinate system.Every point on the plane is represented by a complex number
The Barnsley fern is an example of a fractal. A fractal is an infinitely complex pattern created by iteration: repeating a process over and over in an ongoing feedback loop. One of the most famous and intriguing fractals is the Mandelbrot set, named after the French mathematician Benoît Mandelbrot, who lived from 1924 to 2010. The Mandelbrot set looks like a cardioid, or heart-shaped figure, studded with circles all around its boundary.Like the Barnsley fern, we can create the Mandelbrot set by repeatedly evaluating a simple equation over and over. This equation uses complex numbers. The plane of complex numbers is similar to a two dimensional coordinate system.Every point on the plane is represented by a complex number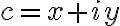 , and we perform the following steps for every point:
, and we perform the following steps for every point:
- Starting with
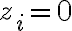 , we create an infinite sequence of complex numbers
, we create an infinite sequence of complex numbers 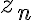 according to the rule
according to the rule 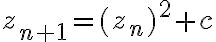
- If this sequence increases to infinity (it diverges), we color the point
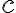 white. If the sequence does not increase beyond a certain limit (it is bounded), we color the point black.
white. If the sequence does not increase beyond a certain limit (it is bounded), we color the point black. - We create a sequence for every point
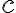 in the plane. The collection of all the black points is the Mandelbrot set. It sits in the portion of the plane where
in the plane. The collection of all the black points is the Mandelbrot set. It sits in the portion of the plane where 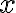 is between
is between 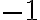 and
and 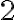
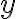 is between
is between  and
and 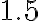
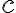 cause the sequence to go to infinity, and the color of the point is proportional to the speed at which the sequence diverges.
cause the sequence to go to infinity, and the color of the point is proportional to the speed at which the sequence diverges.
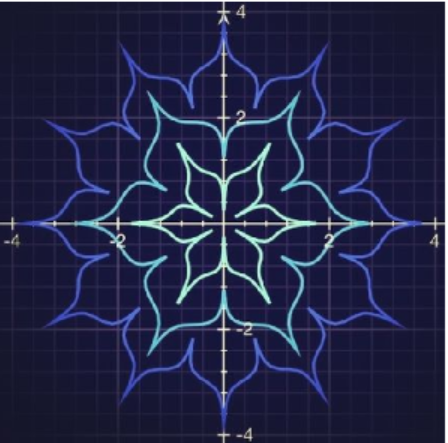
Because the calculations must be performed thousands or millions of times, we need computers to study them. The higher the number of iterations, the better the quality of the image produced. Not coincidentally, the Mandelbrot set was discovered in 1980, shortly after the invention of the personal computer. One of the intriguing features of fractal images is self-similarity. If we zoom in on a fractal, we see the same pattern repeated again and again, sometimes with interesting variations. You can see the copy of whole set embedded in the image. Fractal patterns seem familiar because the laws that govern the creation of fractals are found throughout the natural world. Tree branches, rivers, ice crystals, and seashells all form in fractal shapes.Image Caption: Trigonometric functions as parametric equations can draw beautiful symmetric polar graphs like the one shown.(Content & Image Source: Chapter 10 Introduction, Trigonometry, Katherine Yoshiwara, GNU Free Documentation License)
Upon completion of this module, you will be able to:10.1 Polar Coordinates-
Plot points in polar coordinates
-
Write polar coordinates for points
-
Convert Cartesian coordinates to polar
-
Convert Polar coordinates to Cartesian
-
Write alternate versions of polar coordinates
-
Sketch a region described by polar inequalities
-
Write polar inequalities to describe a region
-
Convert an equation to Cartesian coordinates
-
Convert an equation to polar coordinates
10.2 Polar Graphs-
Describe the effect of parameters in polar curves
-
Compare polar and Cartesian graphs
-
Sketch standard polar graphs
-
Identify standard polar graphs
-
Write equations for standard polar graphs
-
Find intersection points of polar graphs
10.3 Complex Numbers-
Write and simplify complex numbers
-
Perform arithmetic operations on complex numbers
-
Evaluate polynomials at complex numbers, expand polynomials
-
Graph complex numbers
-
Find a polynomial with given zeros
10.4 Polar Form for Complex NumbersTo achieve these objectives:-
Convert from polar form to standard form
-
Write a complex number in polar form
-
Find the product or quotient of two complex numbers in polar form
-
Find a power of a complex number
-
Find the complex roots of a number
- Read the Module 10 Introduction (see above).
- Read Sections 10.1-10.4 of Chapter 10: Polar Form for Complex Numbers in Trigonometry (links to each Section provided below)
- Note: The Algebra Refresher at the top of each Section might be beneficial before you begin
- At the end of each Section there is a list of Vocabulary, Concepts, Study Questions, and a Self-Check H5P activity
- Complete the MyOpenMath Homework Assignments for each Section (links provided below) - These are graded!
- View the Chapter 10 Summary and Review (link provided below)
- Practice the problems on the Exercises Sections, checking the solutions provided (links to each Section provided below)
- View the Exercises: Chapter 10 Review Problems (link provided below)
- Complete the MyOpenMath Quiz for Chapter 10 (link provided below) - This is graded!
- Once you complete the Quiz, upload your work in the Quiz Work Upload Assignment using the submission link below.
- Post in the Chapter 10 Q&A Discussion Forum - link provided below.
Note the check boxes to the right that help you track your progress: some are automatic, and some are manual.
Module Pressbooks Resources and Activities
You will find the following resources and activities in this module at the Pressbooks website. Click on the links below to access or complete each item.
- Starting with
Background Colour
Font Face
Font Kerning
Font Size
Image Visibility
Letter Spacing
Line Height
Link Highlight
Text Colour